Tutorial 1 - Sudoku | Topcoder Quantum Computing Challenge Series

Tutorial #1 - Sudoku

Prerequisite

Python 3.6 running environment

Problem Overview

The challenge phase for this "Tutorial #1 - Sudoku" has ended.
This page is provided as a reference. You can also find our version of entire script at the end of this page.

Sudoku (https://en.wikipedia.org/wiki/Sudoku) is a well-known number puzzle. There are numbers of algorithms to solve Sudoku as explained here: “Mathematics of Sudoku” ( https://en.wikipedia.org/wiki/Mathematics_of_Sudoku), and we will be using DA to solve this puzzle instantly.

With this challenge, you will learn how to turn the Sudoku problem into the QUBO formulation using one of the hardest Sudoku problems as example ( https://www.telegraph.co.uk/news/science/science-news/9359579/Worlds-hardest-sudoku-can-you-crack-it.html)

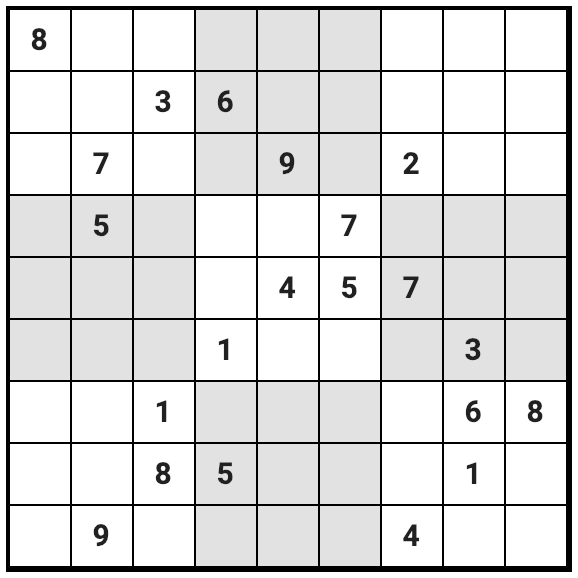
Creating Objective Function

Step 1) Define Solution Model

As mentioned, current DA can solve up to 8192 bits of solution space. We will be limiting the use to 1024 bits for this tutorial.

For Sudoku, there are 9x9 cells where each cell can take numbers from 1 to 9, making 9x9x9 = 729 cells total that can be expressed in 0 or 1 to represent each number which will fit into the solution space.

This solution model is expressed as follows;

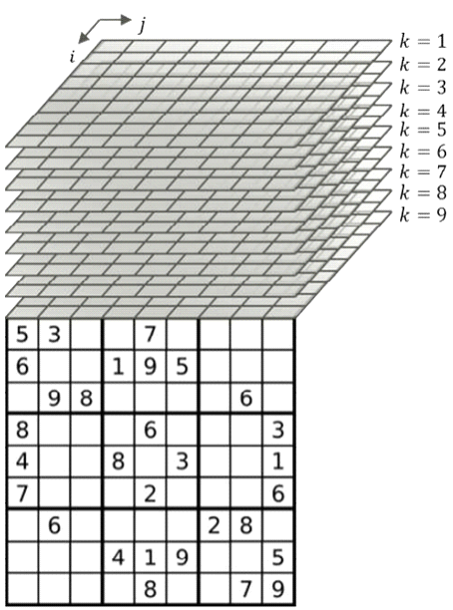
We define that X_ijk will represent each cell in 9x9x9 solution model.

Where

i is the row number from 1 to 9
j is the column number from 1 to 9
k is the number of each cell, from 1 to 9 also

Each X_ijk can have value of 0 or 1.

In the Python implementation, please make sure you have the correct variable numbering:

<i, j, k> → ((i - 1) * 9 + (j - 1)) * 9 + k - 1.

For example of the above, the bottom right cell has a number of 9.Within 9x9x9 solution model, this means that X₉₉₉ = 1, and all other cells of i=9 and j=9 are set to 0 (zero).

As you can imagine, since Sudoku can only have 1 number in a single cell, once some bit in the k is set to 1, all other vertical k cells of the same i and j must be 0.

Step 2) Define the constraints

This will be the key step to solve a problem using DA. You must define all constraints that the problem can potentially take, and create mathematical formulae for them.

For Sudoku, there will be 5 constraints from the rule of the puzzle.

A single cell can only have 1 number
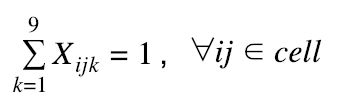
Each column-j cannot have any duplicate number
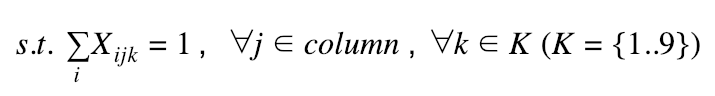
Each row-i cannot have any duplicate number
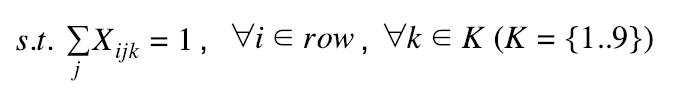
Each of the nine 3x3 subgrids cannot have any duplicate number
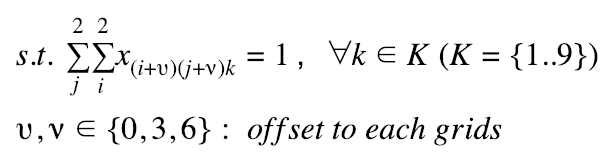
Initial numbers given as “hint” cannot be changed

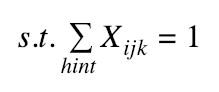
Step 3) Transform into the QUBO formulation

We will now transform the constraints into the QUBO formulation as below;

A single cell can only have 1 number. Here, we introduce a penalty weight α.
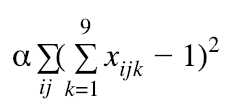
Each column-j can not have a duplicate number
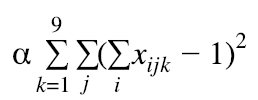
Each row-i cannot have a duplicate number
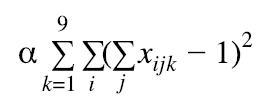
Each of the nine 3x3 subgrids can not have a duplicate number
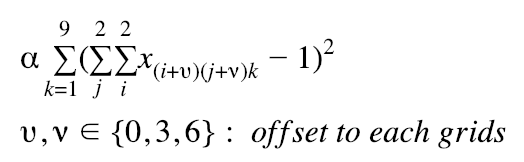
Initial numbers given as “hint” cannot be changed

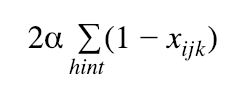
Step 4) The final Objective Function

From Step 2 to 3, we can now define the final objective function that DA must compute

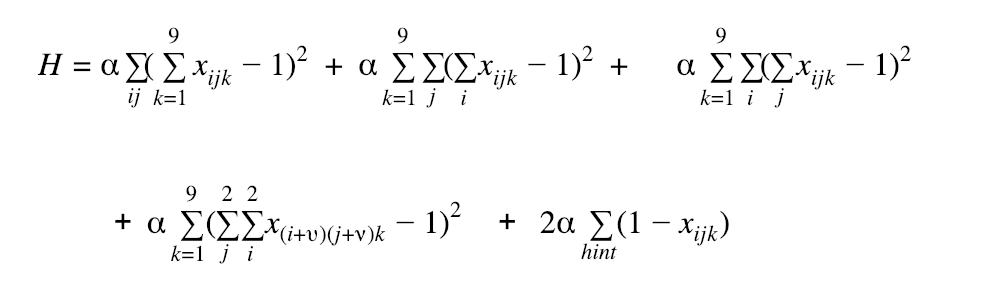
equation

The solution is the minimum combinatorial value of H, where

x_ijk ∈ {0,1} (i,j,k =1..9)

We are using the same penalty value in this formulation. In other problems, you can try to use different weights for different terms if there magnitudes vary.

Coding in Python

As we have defined the Objective Function (H) at the previous step, we will now begin to code the solution in Python.

Step 1) Create initial hints. The format: (column, row, digit); they are all from 0 to 8.

                
hint_hardest = [
    (0, 0, 7),
    (1, 2, 6), (1, 3, 4), (1, 8, 8),
    (2, 1, 2), (2, 6, 0), (2, 7, 7),
    (3, 1, 5), (3, 5, 0), (3, 7, 4),
    (4, 2, 8), (4, 4, 3),
    (5, 3, 6), (5, 4, 4),
    (6, 2, 1), (6, 4, 6), (6, 8, 3),
    (7, 5, 2), (7, 6, 5), (7, 7, 0),
    (8, 6, 7)
]

file_copy

Step 2) Create a Helper Object that can be used to define QUBO

We’ll use the following helper object to build QUBO. In addition, we provide an example of our variable ID generator.

There is an important observation before we write the code: when x is binary, x^2 and x are equivalent. This is extremely useful in the later development. Please keep this in your mind.

                
import numpy as np
from math import sqrt
import copy

class BinaryQuadraticPolynomial:
    '''Quadratic Polynomial class
       Arguments:
           n:                 The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
       Attributes:
           array:             The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary, x_i and x_i * x_i are the same variable.
           constant:          The constant value of this quadratic polynomial.
    '''
    def __init__(self, n=1024):

        self.array = np.zeros((n, n), dtype=int)
        self.constant = 0
        self._size = n

    def export_dict(self):
        '''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
        cells = np.where(self.array != 0)
        ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
        if self.constant != 0:
            ts.append({"coefficient": float(self.constant), "polynomials": []})
        return {'binary_polynomial': {'terms': ts}}

    def add_coef(self, i, j, c):

        if i > j: # make sure it is an upper triangle matrix.
            t = i
            i = j
            j = t
        assert i >= 0, '[Error] Index out of boundary!'
        assert j < self._size, '[Error] Index out of boundary!'
        self.array[i][j] += c

    def add_constant(self, c):

        self.constant += c

    def add_poly(self, other_quad_poly):

        assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
        self.array += other_quad_poly.array
        self.constant += other_quad_poly.constant

    def multiply_constant(self, c):

        self.array *= c
        self.constant *= c

    def finalize(self):

        return copy.deepcopy(self)

                
def get_variable_id(N, i, j, k):

    return (i * N + j) * N + k

file_copy

Step 3) Build Objective Function

In all these rule preparation, we will leave the multiplication of the penalty factor at the end.

1.A single cell can only have 1 number

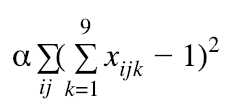
equation

                
def build_cell_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for i in range(N):
        for j in range(N):
            for k1 in range(N):
                var1 = get_variable_id(N, i, j, k1)
                for k2 in range(N):
                    var2 = get_variable_id(N, i, j, k2)
                    rule.add_coef(var1, var2, 1)
                rule.add_coef(var1, var1, -2) # this is -2 * x_{var1}
            rule.add_constant(1)
    return rule.finalize()

file_copy

2.Each column can not have a duplicate number

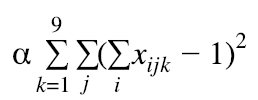
equation

                
def build_column_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for k in range(N):
        for j in range(N):
            for i1 in range(N):
                var1 = get_variable_id(N, i1, j, k)
                for i2 in range(N):
                    var2 = get_variable_id(N, i2, j, k)
                    rule.add_coef(var1, var2, 1)
                rule.add_coef(var1, var1, -2) # this is -2 * x_{var1}
            rule.add_constant(1)
    return rule.finalize()

file_copy

3.Each row cannot have a duplicate number

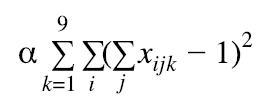
equation

This part is quite similar to the column rule. We leave this part as your exercise.

                
def build_row_rule():
    rule = BinaryQuadraticPolynomial(N * N * N)
    # TODO
    return rule.finalize()

file_copy

4.Each of the nine 3x3 subgrids can not have a duplicate number

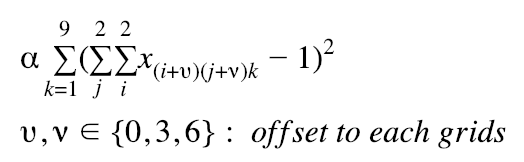
equation

                
def build_subgrid_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    sqrtN = int(sqrt(N))
    for grid_i in range(sqrtN):
        for grid_j in range(sqrtN):
            for k in range(N):
                # there can be only one k in the same subgrid.
                for i1 in range(grid_i * 3, grid_i * 3 + 3):
                    for j1 in range(grid_j * 3, grid_j * 3 + 3):
                        var1 = get_variable_id(N, i1, j1, k)
                        for i2 in range(grid_i * 3, grid_i * 3 + 3):
                            for j2 in range(grid_j * 3, grid_j * 3 + 3):
                                var2 = get_variable_id(N, i2, j2, k)
                                rule.add_coef(var1, var2, 1)
                        rule.add_coef(var1, var1, -2) # this is -2 * x_{var1}
                rule.add_constant(1)
    return rule.finalize()

file_copy

5.Initial numbers given as “hint” cannot be changed

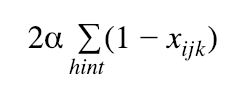
equation

                
def build_hint_rule(N, hint):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for (j, i, k) in hint:
        var =  get_variable_id(N, i, j, k)
        rule.add_coef(var, var, -1) # this is -1 * x_{var}
        rule.add_constant(1)

    return rule.finalize()

file_copy

Step 5) Aggregate and Run on DA

Since DA API is not opened to public, you must call `solveDA` function with BinaryQuadraticPolynomial object as the parameter. This `solveDA` will be swapped to make actual call to DA API when you submit your code.

                
def build_sudoku_rule(N, A):

    cell_rule = build_cell_rule(N)
    row_rule = build_row_rule(N)
    column_rule = build_column_rule(N)
    subgrid_rule = build_subgrid_rule(N)

    cell_rule.multiply_constant(A)
    row_rule.multiply_constant(A)
    column_rule.multiply_constant(A)
    subgrid_rule.multiply_constant(A)

    soduku_rule = BinaryQuadraticPolynomial(N * N * N)
    soduku_rule.add_poly(cell_rule)
    soduku_rule.add_poly(row_rule)
    soduku_rule.add_poly(column_rule)
    soduku_rule.add_poly(subgrid_rule)

    return soduku_rule.finalize()


def build_puzzle_rule(N, A, hint):

    soduku_rule = build_sudoku_rule(N, A)
    puzzle_rule = build_hint_rule(N, hint)
    puzzle_rule.multiply_constant(2 * A)
    puzzle_rule.add_poly(soduku_rule)
    return puzzle_rule.finalize()


def solveDA(rule):
    '''This is a placeholder'''
    return rule.export_dict()


def main(N, hint, A = 1):
    puzzle_rule = build_puzzle_rule(N, A, hint)
    result = solveDA(puzzle_rule)  # Call DA API and return result.
    return result  # Return the result of solveDA function.

file_copy

During the evaluation, we will call your `main` function with hint_hardest to execute your script.
To run your script locally, add following to verify your script;

                
if __name__ == "__main__":
    main(9, hint_hardest, 1)

file_copy

Note on Submissions

Create a single python script file, zip it, and submit to Topcoder platform during the submission phase. The platform will run your script and return the results via email. Make sure that your email registered with Topcoder is accurate and up to date.

Due to how platform is hooked up with DA API, your scripts will be run one by one with other participants’ script. This means that your script will be put in a FIFO queue to run, and you might not be getting the results back immediately.

Following are several rules that apply to this challenge;

You can only run scripts that are intended to solve the provided learning challenges and the Marathon Match. The platform will be checking if your scripts are making the same expected call to DA API for the learning challenges. Initial Sudoku hint also needs to be the same for this tutorial submission.
Each member can make maximum of 10 submissions for this challenge.
The first 30 members to win a prize will be chosen after the submission phase is over.
DA is scheduled to have maintenance downtime on Feb. 7th JST (Feb. 6th 10am to 7th 10am EST). If you submit during this time, your submission will be queued and executed after the maintenance.

Once you have submitted the script, the system will send you an email that it has successfully received your script. After your script has been executed, the system will send you another email with results. When successful, the result of DA API will be provided in addition to the Sudoku puzzle that got solved. In case of error you will see a message of possible reasons, please try again to re-submit.

Please ask in the challenge forums if there are any questions.

Misc. Notes

As seen, DA can take QUBO formulation and solve the problem at stake.
There are many algorithm to solve Sudoku. But as we've shown in this tutorial, you can easily change the rules like variation of grid sizes or imposing additional constraints such as making main diagonals to also be unique, instantly.
This is especially useful in solving real-world problems and we will be showing you some scheduling problem in the next learning challenge.

Proposed Solution

As the submission phase for this tutorial #1 has ended, we are showing the proposed entire script provided for your reference.

                
import json
import numpy as np
from math import sqrt
import copy

hint_hardest = [
    (0, 0, 7),
    (1, 2, 6), (1, 3, 4), (1, 8, 8),
    (2, 1, 2), (2, 6, 0), (2, 7, 7),
    (3, 1, 5), (3, 5, 0), (3, 7, 4),
    (4, 2, 8), (4, 4, 3),
    (5, 3, 6), (5, 4, 4),
    (6, 2, 1), (6, 4, 6), (6, 8, 3),
    (7, 5, 2), (7, 6, 5), (7, 7, 0),
    (8, 6, 7)
]

class BinaryQuadraticPolynomial:
    '''Quadratic Polynomial class
       Arguments:
           n:                 The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
       Attributes:
           array:             The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary, x_i and x_i * x_i are the same variable.
           constant:          The constant value of this quadratic polynomial.
    '''
    def __init__(self, n=1024):

        self.array = np.zeros((n, n), dtype=int)
        self.constant = 0
        self._size = n

    def export_dict(self):
        '''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
        cells = np.where(self.array != 0)
        ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
        if self.constant != 0:
            ts.append({"coefficient": float(self.constant), "polynomials": []})
        return {'binary_polynomial': {'terms': ts}}

    def add_coef(self, i, j, c):

        if i > j: # make sure it is an upper triangle matrix.
            t = i
            i = j
            j = t
        assert i >= 0, '[Error] Index out of boundary!'
        assert j < self._size, '[Error] Index out of boundary!'
        self.array[i][j] += c

    def add_constant(self, c):

        self.constant += c

    def add_poly(self, other_quad_poly):

        assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
        self.array += other_quad_poly.array
        self.constant += other_quad_poly.constant

    def multiply_constant(self, c):

        self.array *= c
        self.constant *= c

    def finalize(self):

        return copy.deepcopy(self)


def get_variable_id(N, i, j, k):

    return (i * N + j) * N + k


def build_cell_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for i in range(N):
        for j in range(N):
            for k1 in range(N):
                var1 = get_variable_id(N, i, j, k1)
                for k2 in range(N):
                    var2 = get_variable_id(N, i, j, k2)
                    rule.add_coef(var1, var2, 1)
                rule.add_coef(var1, var1, -2)  # this is -2 * x_{var1}
            rule.add_constant(1)
    return rule.finalize()


def build_row_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for k in range(N):
        for i in range(N):
            for j1 in range(N):
                var1 = get_variable_id(N, i, j1, k)
                for j2 in range(N):
                    var2 = get_variable_id(N, i, j2, k)
                    rule.add_coef(var1, var2, 1)
                rule.add_coef(var1, var1, -2)  # this is -2 * x_{var1}
            rule.add_constant(1)
    return rule.finalize()


def build_column_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for k in range(N):
        for j in range(N):
            for i1 in range(N):
                var1 = get_variable_id(N, i1, j, k)
                for i2 in range(N):
                    var2 = get_variable_id(N, i2, j, k)
                    rule.add_coef(var1, var2, 1)
                rule.add_coef(var1, var1, -2)  # this is -2 * x_{var1}
            rule.add_constant(1)
    return rule.finalize()


def build_subgrid_rule(N):

    rule = BinaryQuadraticPolynomial(N * N * N)
    sqrtN = int(sqrt(N))
    for grid_i in range(sqrtN):
        for grid_j in range(sqrtN):
            for k in range(N):
                # there can be only one k in the same subgrid.
                for i1 in range(grid_i * 3, grid_i * 3 + 3):
                    for j1 in range(grid_j * 3, grid_j * 3 + 3):
                        var1 = get_variable_id(N, i1, j1, k)
                        for i2 in range(grid_i * 3, grid_i * 3 + 3):
                            for j2 in range(grid_j * 3, grid_j * 3 + 3):
                                var2 = get_variable_id(N, i2, j2, k)
                                rule.add_coef(var1, var2, 1)
                        rule.add_coef(var1, var1, -2)  # this is -2 * x_{var1}
                rule.add_constant(1)
    return rule.finalize()

def build_hint_rule(N, hint):

    rule = BinaryQuadraticPolynomial(N * N * N)
    for (j, i, k) in hint:
        var = get_variable_id(N, i, j, k)
        rule.add_coef(var, var, -1)  # this is -1 * x_{var}
        rule.add_constant(1)

    return rule.finalize()


def build_sudoku_rule(N, A):

    cell_rule = build_cell_rule(N)
    row_rule = build_row_rule(N)
    column_rule = build_column_rule(N)
    subgrid_rule = build_subgrid_rule(N)

    cell_rule.multiply_constant(A)
    row_rule.multiply_constant(A)
    column_rule.multiply_constant(A)
    subgrid_rule.multiply_constant(A)

    soduku_rule = BinaryQuadraticPolynomial(N * N * N)
    soduku_rule.add_poly(cell_rule)
    soduku_rule.add_poly(row_rule)
    soduku_rule.add_poly(column_rule)
    soduku_rule.add_poly(subgrid_rule)

    return soduku_rule.finalize()



def build_puzzle_rule(N, A, hint):

    soduku_rule = build_sudoku_rule(N, A)
    # print(soduku_rule.export_dict())
    puzzle_rule = build_hint_rule(N, hint)
    puzzle_rule.multiply_constant(2 * A)
    puzzle_rule.add_poly(soduku_rule)
    # print(puzzle_rule.export_dict())
    return puzzle_rule.finalize()


def solveDA(rule):
    '''This is a placeholder'''
    print(json.dumps(rule.export_dict()))


def main(N, hint, A=1):
    puzzle_rule = build_puzzle_rule(N, A, hint)
    print(puzzle_rule)
    return solveDA(puzzle_rule)  # wrapper to call DA API and return results.

if __name__ == "__main__":
    main(9, hint_hardest, 1)

file_copy