Tutorial #3 - Max Cut
Prerequisite
- Python 3.6 running environment
Problem Overview
The challenge phase for this "Tutorial #3 - Max Cut" has ended.
This page is provided as a reference. You can also find our version of entire script at the end of this page.
Maximum Cut (https://en.wikipedia.org/wiki/Maximum_cut) is a well-known NP-complete problem. Its weighted version is one of Karp's 21 NP-complete problems (https://en.wikipedia.org/wiki/Karp%27s_21_NP-complete_problems). In this learning challenge, we will be using DA to solve this puzzle instantly.
If you didn’t participate in the previous learning challenges, please have a check first.
In the weighted maximum cut problem, we are going to partition the nodes into two parts and maximize the total edge weights between the two parts. An edge is “between the two parts” if and only if its two nodes belong to the two parts respectively.
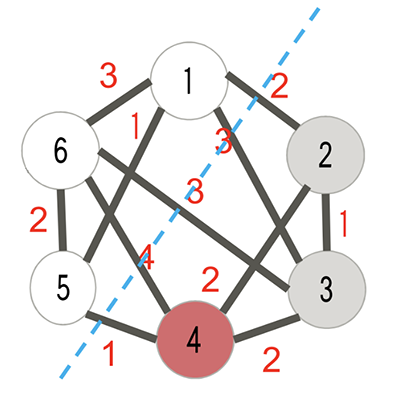
Problem Formulation
You must define all objective functions and all constraints that the problem can potentially take and create mathematical formulae for them.
This problem can be formulated as following: \[ maximize \sum_{i \in S, j \not\in S}d_{i,j}: S \subseteq V \]
Transform into QUBO formulation
This will be the key step to solve a problem using DA.
you must define boolean variables and transform all objective functions and constraints into QUBO formulation.
Step 1) Define Solution Model
As mentioned, DA can solve up to 8192 bits of solution space. We will be limiting the use to 1024 bits for this tutorial.
For Max-Cut, there are N nodes where each node can be put into one of the two parts.
We can define a boolean variable for each node, representing whether it belongs to
the first part. As long as the number of nodes is no more than 1024, it will fit
into the solution space.
For this tutorial, we will be using a dataset that has 800 nodes. You can safely assume
that all test cases will fit into the solution space and create QUBO only thinking about
800 nodes.
This solution model is expressed as follows;
We define that \(x_i\) will represent the i-th node (numbered from 1 to N) the solution model.
Each \(x_i\) can have value of 0 or 1, representing whether this node belongs to the first part
in the partition.
In the Python implementation, please make sure you have the correct variable numbering:
Step 2) Define the Objective Function
For Max-cut, there is only one objective function that represents
the total edge weights between the two parts.
Note that in DA, we are always minimizing the objective function.
So we turn the objective into the following one. Also, we will not be needing
penalty weight like the previous challenges.
\[ - \sum_{(i,j) \ is \ an \ edge} d_{i,j} (x_i - x_j) ^ 2 \]
Step 3) The final Objective Function
From above, we can now define the final objective function that DA must compute
\[ H = - \sum_{(i,j) \ is \ an \ edge} d_{i,j} (x_i - x_j) ^ 2 \]
The solution is the minimum combinatorial value of H, where \( x_i \in {0,1} (i = 1..N) \)
DA API Parameters
For this tutorial, you will be learning about the parameters you can pass to
DA API to get the best results back, and the format of response.
(Until the last tutorial, these parameters were hard-coded inside the platform)
API Request
DA API has several modes, which are called “solvers”, that it can use to solve QUBO.
For this tutorial and upcoming Marathon Match, we will be using a solver called
DA2PTSolver, which will automatically try to resolve many of the parameters that you
can actually specify.
(Note: There are other solvers that can do fine-tuning thus having
less annealing time to find an optimal solution. We will be
using the DA2PTSolver for simplicity for the tutorial and Marathon Match)
For this DA2PTSolver, there are only 4 parameters that you will need to know. You can pass these parameters to ‘solveDA’ function explained at “Coding in Python” section below.
| Parameter | Description |
|---|---|
| number_iterations |
The number of searches per anneal (int32 type). |
| number_replicas |
The number of replicas (int32 type). |
| guidance_config |
Initial value of each variable ("uint32 type":boolean type). |
| solution_mode |
Optimal solution return mode (string type). |
There is also a limit that:
(number _replicas * number_iterations) needs to be greater or equals to 100,000 and less or equals to 100,000,000,000
Other Notes and Limitations:
- The time required for annealing (anneal_time) is determined by the values specified for the number_iteration and number_replicas. If a value is multiplied by 10, 100, ..., anneal_time is also multiplied by 10, 100, ... in direct proportion. Be careful when specifying a value.
-
The Digital Annealer hardware encodes the coefficient of a binary quadratic polynomial
as an integer. The calculation precision of the Digital Annealer hardware is as follows.
To find the optimal solution, it is necessary to specify coefficients in a QUBO expression
within the range of precision for the Digital Annealer hardware.
- Quadratic Term: 64bit signed integer (The available range is -2^63 to 2^63-1)
- Linear Term: 76bit signed integer
- If a coefficient in a QUBO expression is out of the calculation precision range of the Digital Annealer hardware or is not an integer, DA2PTSovler automatically converts it into a polynomial that can be solved with the Digital Annealer hardware.
- In addition to the hardware limitations, DA API uses the double type for coefficients. In order to not be affected by rounding errors in the double type coefficients (double-precision floating point numbers), it is recommended to set a value within the range from -2^52 to 2^52.
- For the upcoming Marathon Match, the total time taken to run your script will be included in the scoring function. Also, there is a time limit of 60 sec. to run your script. We advise you to try to solve this tutorial with default parameters, then try multiple times with different parameters to understand how it will affect the results and annealing time.
API Response
The API will return the list of Solution, each having the energy, frequency, and configuration
(which is bit array of the answer).
When "QUICK" is specified as request paramenter, the list will have only 1 solution.
Please see "Coding in Python" section for how solveDA function returns the list.
| Key | Description |
|---|---|
| energy | Energy of the optimal solution |
| frequency |
Appearance frequency of the same configuration.
|
| configuration | The solution value for each variable X (true or false) |
Coding in Python
As we have defined the Objective Function (H) at the previous step, we will now begin to code the solution in Python.
We assume the format as; The first line: “N_Nodes N_Edges”. The following N_Edges lines: “Node_i Node_j Weight”.
def load_graph(filename):
lines = open(filename).readlines()
n_node = int(lines[0].split()[0])
n_edge = int(lines[0].split()[1])
assert len(lines) == n_edge + 1
edges = []
for i in range(n_edge):
parts = lines[i + 1].split()
a, b, c = int(parts[0]), int(parts[1]), int(parts[2])
assert (1 <= a) and (a <= n_node)
assert (1 <= b) and (b <= n_node)
a -= 1
b -= 1
edges.append((a, b, c))
return n_node, edges
We’ll use the following helper object to build QUBO.
There is an important observation before we write the code: when x is binary, x^2 and x are equivalent. This is extremely useful in the later development. Please keep this in your mind.
import numpy as np
from math import sqrt
import copy
class BinaryQuadraticPolynomial:
'''Quadratic Polynomial class
Arguments:
n: The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
Attributes:
array: The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary,
x_i and x_i * x_i are the same variable.
constant: The constant value of this quadratic polynomial.
'''
def __init__(self, n = 1024):
self.array = np.zeros((n, n), dtype = int)
self.constant = 0
self._size = n
def export_dict(self):
'''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
cells = np.where(self.array != 0)
ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
if self.constant != 0:
ts.append({"coefficient": float(self.constant), "polynomials": []})
return {'binary_polynomial': {'terms': ts}}
def add_coef(self, i, j, c):
if i > j: # make sure it is an upper triangle matrix.
t = i
i = j
j = t
assert i >= 0, '[Error] Index out of boundary!'
assert j < self._size, '[Error] Index out of boundary!'
self.array[i][j] += c
def add_constant(self, c):
self.constant += c
def add_poly(self, other_quad_poly):
assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
self.array += other_quad_poly.array
self.constant += other_quad_poly.constant
def multiply_constant(self, c):
self.array *= c
self.constant *= c
def finalize(self):
return copy.deepcopy(self)
-
Maximize the total weights between the two parts. Note that in DA, we are always minimizing the objective function.
\[ - \sum_{(i,j) \ is \ an \ edge} d_{i,j} (x_i - x_j) ^ 2 \]
def build_max_cut_rule(n_node, edges): rule = BinaryQuadraticPolynomial(n_node) # TODO return rule.finalize()Click to Copy
Since DA API is not opened to public, you must call "solveDA" with BinaryQuadraticPolynomial object and DA API parameters.
Note that we have introduced new parameter to "solveDA" from previous tutorials to specify the DA API paramenters.
During the evaluation, we will call your “main” function with test case graph to execute your script. We will be checking the 2 groups returned from “main” function if it has successfully made the cut of the graph and calculate the score. Here we introduce “make_max_cut_answer” function to parse da_results and create 2 groups to return.
class Solution:
def __init__(self, energy=0, frequency=0, configuration=[]):
self.energy = energy
self.frequency = frequency
self.configuration = configuration
def solveDA(rule, da_params):
'''This is a placeholder'''
import json
print(json.dumps({
'da_params': da_params,
'rule': rule.export_dict()
}))
dummy_solution = Solution(1, 1, list(np.random.randint(2, size=rule._size)))
return [dummy_solution]
def find_minimum_solution(da_results):
minimum = da_results[0].energy
best_solution = None
for result in da_results:
e = result.energy
s = result
if minimum >= e:
minimum = e
best_solution = s
return best_solution
def make_max_cut_answer(da_results):
# This is an example.
solution = find_minimum_solution(da_results)
group_1 = []
group_2 = []
for i, bit in enumerate(solution.configuration):
if bit == 0:
group_1.append(i + 1)
else:
group_2.append(i + 1)
return group_1, group_2
def main(n_node, edges):
qubo = build_max_cut_rule(n_node, edges)
# wrapper to call DA API.
da_results = solveDA(qubo, {
'number_iterations': 500000,
'number_replicas': 26, # Min: 26, Max: 128
# Start solving using the initial bits.
'guidance_config': {str(x): False for x in range(0, qubo._size)},
'solution_mode': 'COMPLETE' # QUICK or COMPLETE
})
# Return the groups of nodes of the max-cut.
group_1, group_2 = make_max_cut_answer(da_results)
return (group_1, group_2)
To run your script locally, add following to verify your script;
if __name__ == '__main__':
n_node, edges = load_graph('sample_graph.txt')
answer = main(n_node, edges)
print('Group 1', answer[0])
print('Group 2', answer[1])
Create a single python script file, zip it, and submit to Topcoder platform during the submission phase. The platform will run your script and return the results via email. Make sure that your email registered with Topcoder is accurate and up to date.
Due to how platform is hooked up with DA API, your scripts will be run one by one with other participants’ script. This means that your script will be put in a FIFO queue to run, and you might not be getting the results back immediately.
Following are several rules that apply to this challenge;
-
You can only run scripts that are intended to solve the provided learning
challenges and the Marathon Match.
The platform will be checking your scripts and returns error if the number of solution bits do not match what's mentioned in this tutorial.
-
The platform will be checking your script with 2 test cases, and returns error for following:
-
Each member can make maximum of 30 submissions for this challenge.
Please go ahead and try to submit multiple times. - There is a time limit of 60 sec. The system will return error if your script takes more than 60 sec. to execute and find a solution.
- The score needs to be beyond some certain threshold (which are the known highest score for the given datasets)
- The solution bits returned from DA API needs to be 800 (total nodes of every test case passed to your script will be 800)
- The script must cut the given graph into 2 parts
- Your script need to succeed for all 2 test cases in order to win a prize
- DA is scheduled to have maintenance downtime on Mar. 7th JST (Mar. 6th 10am to 7th 10am EST). If you submit during this time, your submission will be queued and executed after the maintenance.
-
Each member can make maximum of 30 submissions for this challenge.
- The first 30 members to win a prize will be chosen after the submission phase is over.
Once you have submitted the script, the system will send you multiple emails that it has
successfully received your script and performed virus checks.
After your script has been executed against DA, the system will send you another email with results from "TC3-QuantumScorer" reviewer.
When execution of your script is successful, overall result and request/response of DA API calls for each test case will be provided.
Note that even though DA API will return multiple Solutions when "COMPLETE" is specified for solution_mode parameter,
the email will have only the first best energy Solution. (We are planning to return all the Solutions for the upcoming
Marathon Match)
In case of error you will see a message of possible reasons, please try again to re-submit.
Please ask in the challenge forums if there are any questions.
Proposed Solution
As the submission phase for this tutorial #3 has ended, we are showing the proposed entire script provided for your reference.
import numpy as np
import copy
'''
Step 1. Load the graph from a file.
'''
def load_graph(filename):
lines = open(filename).readlines()
n_node = int(lines[0].split()[0])
n_edge = int(lines[0].split()[1])
assert len(lines) == n_edge + 1
edges = []
for i in range(n_edge):
parts = lines[i + 1].split()
a, b, c = int(parts[0]), int(parts[1]), int(parts[2])
assert (1 <= a) and (a <= n_node)
assert (1 <= b) and (b <= n_node)
a -= 1
b -= 1
edges.append((a, b, c))
return n_node, edges
'''
Step 2. Create a Helper Object that can be used to define QUBO
'''
class BinaryQuadraticPolynomial:
'''Quadratic Polynomial class
Arguments:
n: The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
Attributes:
array: The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary, x_i and x_i * x_i are the same variable.
constant: The constant value of this quadratic polynomial.
'''
def __init__(self, n = 1024):
self.array = np.zeros((n, n), dtype = int)
self.constant = 0
self._size = n
def export_dict(self):
'''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
cells = np.where(self.array != 0)
ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
if self.constant != 0:
ts.append({"coefficient": float(self.constant), "polynomials": []})
return {'binary_polynomial': {'terms': ts}}
def add_coef(self, i, j, c):
if i > j: # make sure it is an upper triangle matrix.
t = i
i = j
j = t
assert i >= 0, '[Error] Index out of boundary!'
assert j < self._size, '[Error] Index out of boundary!'
self.array[i][j] += c
def add_constant(self, c):
self.constant += c
def add_poly(self, other_quad_poly):
assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
self.array += other_quad_poly.array
self.constant += other_quad_poly.constant
def multiply_constant(self, c):
self.array *= c
self.constant *= c
def finalize(self):
return copy.deepcopy(self)
'''
Step 3. Build Objective Function
'''
def build_max_cut_rule(n_node, edges):
rule = BinaryQuadraticPolynomial(n_node)
for (i, j, dij) in edges:
# dij * (x_i - x_j) ^ 2
rule.add_coef(i, j, -2 * dij)
rule.add_coef(i, i, dij)
rule.add_coef(j, j, dij)
rule.multiply_constant(-1)
return rule.finalize()
class Solution:
def __init__(self, energy=0, frequency=0, configuration=[]):
self.energy = energy
self.frequency = frequency
self.configuration = configuration
def solveDA(rule, da_params):
'''This is a placeholder'''
import json
print(json.dumps({
'da_params': da_params,
'rule': rule.export_dict()
}))
dummy_solution = Solution(1, 1, list(np.random.randint(2, size=rule._size)))
return [dummy_solution]
def find_minimum_solution(da_results):
minimum = da_results[0].energy
best_solution = None
for result in da_results:
e = result.energy
s = result
if minimum >= e:
minimum = e
best_solution = s
return best_solution
def make_max_cut_answer(da_results):
# This is an example.
solution = find_minimum_solution(da_results)
group_1 = []
group_2 = []
for i, bit in enumerate(solution.configuration):
if bit == 0:
group_1.append(i + 1)
else:
group_2.append(i + 1)
return group_1, group_2
def main(n_node, edges):
qubo = build_max_cut_rule(n_node, edges)
# wrapper to call DA API.
da_results = solveDA(qubo, {
'number_iterations': 3500000,
'number_replicas': 52, # Min: 26, Max: 128
# Start solving using the initial bits.
'guidance_config': {str(x): False for x in range(0, qubo._size)},
'solution_mode': 'QUICK' # QUICK or COMPLETE
})
# Return the groups of nodes of the max-cut.
group_1, group_2 = make_max_cut_answer(da_results)
return (group_1, group_2)
# sample_graph.txt
"""
5 4
1 5 1
2 5 1
4 5 1
3 4 1
"""
if __name__ == '__main__':
n_node, edges = load_graph('sample_graph.txt')
answer = main(n_node, edges)
print('Group 1', answer[0])
print('Group 2', answer[1])