Tutorial #2 - Scheduling
Prerequisite
- Python 3.6 running environment
Problem Overview
The challenge phase for this "Tutorial #2 - Scheduling" has ended.
This page is provided as a reference. You can also find our version of entire script at the end of this page.
Scheduling is a real-world task to arrange a time table for the workers to meet the daily production rate requirement. In this learning challenge, we will be using DA to solve this puzzle instantly.
If you didn’t participate in the previous learning challenge about Sudoku, please have a check first.
In the schedule problem, there are A workers, D days, and every day has T slots.
For simplicity of this tutorial, we define that D is always multiple of 7, and in the last, you will be solving the case where A=25, D=7 (1 week), and T=4 (6 hours per shift).
sa is the amount of product that can be produced by the worker a in each shift.
Sd is the amount of product that is desired to be produced on the day d.
radt is a boolean variable that represents whether the worker a is willing to work in the shift t on day d.
The overall goal is to find a D-day schedule that the total amount of product produced on each day is as close as possible to the desired amount.
There are a few more constraints as follows.
-
We cannot force any worker to work if he/she is not willing to do.
-
No worker can work right after the final shift of a day -- they need to sleep. Note that we will repeat the schedule. So the day after D-th day is the 1-st day.
-
Every worker can work at most 1 slot per day
-
Every worker needs at least 2 holidays in a week.
-
We encourage to maximize the utilization of the workers. Therefore, we try to avoid employing any worker that only works 1 day per week. And we try to minimize the number of workers that works more than 1 day.
We will discuss how to implement these constraints in the following sections.
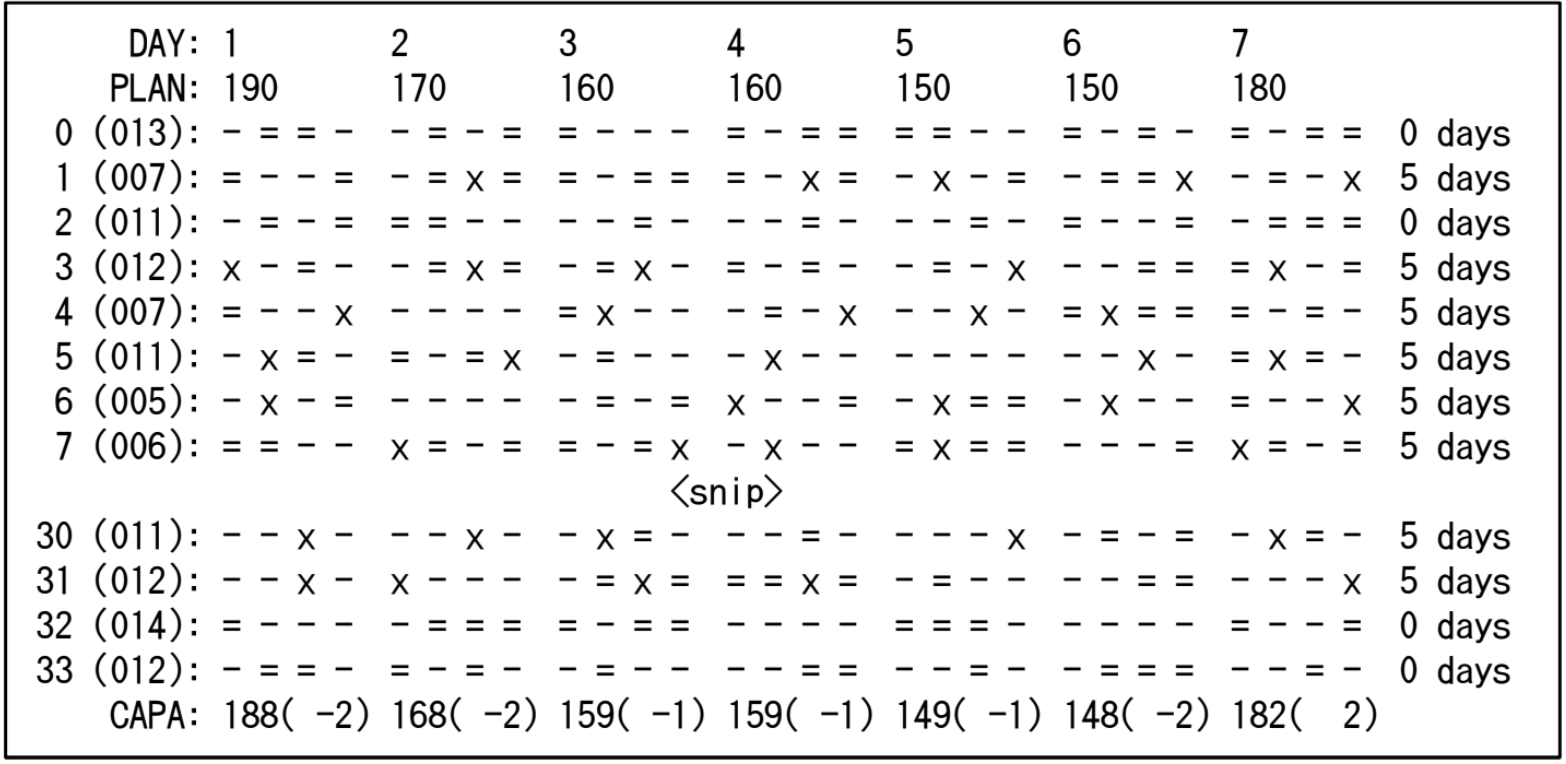
The final formatted solution will look like following where "x" denotes the shift calculated,
"=" denotes the slot that the workers were willing to work, "-" denotes the slot that the workers not willing to work,
and each worker's sa in parentheses.
Creating Objective Function
Step 1) Define Solution Model
As mentioned, DA can solve up to 8192 bits of solution space. We will be limiting the use to 1024 bits for this tutorial.
For Scheduling, it is natural to use Xadt to represent whether the worker a will work in the shift t on day d. We also introduce some auxiliary variables Yaw0 and Yaw1. We will explain the purpose and usage of these auxiliary variables later. So as long as \( ((A * D * T) + (2 * A * (D / 7)) \leqq 1024 \), it will fit into the solution space. Note that \((2 * A * (D / 7))\) is a space necessary for auxiliary variables.
This solution model is expressed as follows;
In the Python implementation, please make sure you have the correct variable numbering ("w" denotes number of weeks):
Step 2) Define the constraints and Transform into the QUBO formulation
This will be the key step to solve a problem using DA. You must define all constraints that the
problem can potentially take, and create mathematical formulae for them.
For formulae 2 to 6, we introduce a penalty weight W. For simplicity of this tutorial, W will be the same for all 5 formulae.
-
The overall goal is to find a D-day schedule that the total amount of product produced on each day is as close as possible to the desired amount.
\[ \sum_d ( \sum_{a,t} s^a X_{adt} - S^d)^2 \]
-
We cannot force any worker to work if he/she is not willing to do.
\[ W \sum_{adt} (1 - r^{adt} ) X_{adt}\\ r^{adt} \in {0, 1} \]
-
No worker can work right after the final shift of a day -- they need to sleep. Note that we will repeat the schedule. So the day after D-th day is the 1-st day.
\[ W \sum_{ad} X_{adT} X_{a(d+1)0} \]
-
Every worker can work at most 1 slot per day.
\[ W \sum_{ad} ( \sum_t X_{adt} )( \sum_t X_{adt} - 1) \]
-
Every worker needs at least 2 holidays in a week. Here we will use the auxiliary variables.
\[ W \sum_{w=1 \ to \ D/7} \sum_a ( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} + 2y_{aw0} + 5y_{aw1} - 4 ) ( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} + 2y_{aw0} + 5y_{aw1} - 5) \]
The auxiliary variables can adjust their values according to \( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} \) to make sure that there is no penalty. If you enumerate the 4 possible combinations of Yaw0 and Yaw1, you will find out that they can cover the cases of 0, 2, 3, 4, 5.
There would be other ways to express the constraint using more auxiliary variables, but as you can see here, we have defined the formulation to just use 2 variables, in order to minimize the limited solution space (1024 bits).
-
We encourage to maximize the utilization of the workers. Therefore, we try to avoid employing any worker that only works 1 day per week. And we try to minimize the number of workers that works more than 1 day.
\[ -W \sum_{w=1 \ to \ D/7} \sum_a y_{aw1} \]
In the previous enumeration, you can find out that when \( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} = 0 \), \(y_{aw1}\) will be 1.
Step 3) The final Objective Function
We can now define the final objective function that DA must compute as the sum of every term we derived in Step 2).
Coding in Python
As we have defined the Objective Function at the previous step, we will now begin to code the solution in Python.
def generate_test_case(D, A, T, seed):
'''There are D days, A workers, T time slots per day, and the random seed is seed'''
assert D % 7 == 0, '[Error] D must be a multiple of 7 days'
np.random.seed(seed)
worker_skill = np.random.randint(5, 15, size = A)
# print 'worker_skill:', worker_skill
daily_workload = np.random.randint(15, 20, size=D)
daily_workload = 10 * daily_workload
# print 'daily_workload:', daily_workload
reqs = np.random.randint(2, size =(A, D, T))
W = np.max(daily_workload) // 2
# print 'W:', W
return worker_skill, daily_workload, reqs, W
We’ll use the following helper object to build QUBO. In addition, we provide an example of our variable ID generator.
There is an important observation before we write the code: when x is binary, x^2 and x are equivalent. This is extremely useful in the later development. Please keep this in your mind.
import numpy as np
from math import sqrt
import copy
class BinaryQuadraticPolynomial:
'''Quadratic Polynomial class
Arguments:
n: The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
Attributes:
array: The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary,
x_i and x_i * x_i are the same variable.
constant: The constant value of this quadratic polynomial.
'''
def __init__(self, n = 1024):
self.array = np.zeros((n, n), dtype = int)
self.constant = 0
self._size = n
def export_dict(self):
'''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
cells = np.where(self.array != 0)
ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
if self.constant != 0:
ts.append({"coefficient": float(self.constant), "polynomials": []})
return {'binary_polynomial': {'terms': ts}}
def add_coef(self, i, j, c):
if i > j: # make sure it is an upper triangle matrix.
t = i
i = j
j = t
assert i >= 0, '[Error] Index out of boundary!'
assert j < self._size, '[Error] Index out of boundary!'
self.array[i][j] += c
def add_constant(self, c):
self.constant += c
def add_poly(self, other_quad_poly):
assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
self.array += other_quad_poly.array
self.constant += other_quad_poly.constant
def multiply_constant(self, c):
self.array *= c
self.constant *= c
def finalize(self):
return copy.deepcopy(self)
def get_variable_id(D, A, T, d, a, t):
'''x_{a,d,t}'''
return (d * A + a) * T + t
def get_variable_id_y(D, A, T, a, w, p):
'''y_{a,w,p=0/1}'''
return A * D * T + (w * A + a) * 2 + p
def get_total_variables(D, A, T):
return D * A * T + D // 7 * A * 2
In this challenge, the objective function is rather complicated. We will go through most of them together and leave a small part to you for the exercise. In all these rule preparation, we will leave the multiplication of the penalty factor at the end.
-
The overall goal is to find a D-day schedule that the total amount of product produced on each day is as close as possible to the desired amount.
\[ \sum_d ( \sum_{a,t} s^a X_{adt} - S^d)^2 \]
def build_total_workload_rule(D, A, T, worker_skill, daily_workload): rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T)) for d in range(D): # (sum(s_a x_{a,d,t}) - S_d)^2 S_d = daily_workload[d] for t1 in range(T): for a1 in range(A): var1 = get_variable_id(D, A, T, d, a1, t1) s_a1 = worker_skill[a1] for t2 in range(T): for a2 in range(A): var2 = get_variable_id(D, A, T, d, a2, t2) s_a2 = worker_skill[a2] # s_a1 * s_a2 * x_{var1} * x_{var2} rule.add_coef(var1, var2, s_a1 * s_a2) # this is for -2 S_d s_a1 x_{var1} rule.add_coef(var1, var1, - 2 * s_a1 * S_d) rule.add_constant(S_d * S_d) return rule.finalize()Click to Copy -
We cannot force any worker to work if he/she is not willing to do. Here, we introduce a penalty weight W.
\[ W \sum_{adt} (1 - r^{adt} ) X_{adt}\\ r^{adt} \in {0, 1} \]
def build_preferred_time_rule(D, A, T, reqs): rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T)) for d in range(D): for t in range(T): for a in range(A): var = get_variable_id(D, A, T, d, a, t) # this is for (1 - reqs[a][d][t]) * x_{var} rule.add_coef(var, var, 1 - reqs[a][d][t]) return rule.finalize()Click to Copy -
No worker can work right after the final shift of a day -- they need to sleep. Note that we will repeat the schedule. So the day after D-th day is the 1-st day.
\[ W \sum_{ad} X_{adT} X_{a(d+1)0} \]
This one is really simple. So we leave it to you for the exercise.
def build_sleep_rule(D, A, T): rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T)) # TODO return rule.finalize()Click to Copy -
Every worker can work at most 1 slot per day.
\[ W \sum_{ad} ( \sum_t X_{adt} )( \sum_t X_{adt} - 1) \]
def build_workonce_rule(D, A, T): rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T)) for d in range(D): for a in range(A): # sum(x_{a, d, t}) * (sum(x_{a, d, t}) - 1) for t1 in range(T): var1 = get_variable_id(D, A, T, d, a, t1) for t2 in range(T): var2 = get_variable_id(D, A, T, d, a, t2) rule.add_coef(var1, var2, 1) # this is for -x_{var1} rule.add_coef(var1, var1, -1) return rule.finalize()Click to Copy -
Every worker needs at least 2 holidays in a week. Here we will use the auxiliary variables.
\[ W \sum_{w=1 \ to \ D/7} \sum_a ( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} + 2y_{aw0} + 5y_{aw1} - 4 ) ( \sum_{d=7(w-1)+1 \ to \ 7w} \sum_t X_{adt} + 2y_{aw0} + 5y_{aw1} - 5) \]
-
We encourage to maximize the utilization of the workers. Therefore, we try to avoid employing any worker that only works 1 day per week. And we try to minimize the number of workers that works more than 1 day.
\[ -W \sum_{w=1 \ to \ D/7} \sum_a y_{aw1} \]
We combine the 5) and 6) together in the following function. This one is a little complicated. So we provide you the example implementation.
def build_holiday_rule(D, A, T): # within each week, every worker works at most 5 days. rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T)) for a in range(A): for w in range(D // 7): y0 = get_variable_id_y(D, A, T, a, w, 0) y1 = get_variable_id_y(D, A, T, a, w, 1) coef_y0 = 2 coef_y1 = 5 # (sum(x_{a, d, t}) + 2y0 + 5y1 - 4) * (sum(x_{a, d, t} + 2y0 + 5y1 - 5)) for d1 in range(w * 7, w * 7 + 7): for t1 in range(T): var1 = get_variable_id(D, A, T, d1, a, t1) for d2 in range(w * 7, w * 7 + 7): for t2 in range(T): var2 = get_variable_id(D, A, T, d2, a, t2) rule.add_coef(var1, var2, 1) rule.add_coef(var1, y0, 2 * coef_y0) rule.add_coef(var1, y1, 2 * coef_y1) # this is for (-4 + -5) x_{var1} rule.add_coef(var1, var1, -9) rule.add_coef(y0, y0, coef_y0 * coef_y0) rule.add_coef(y0, y1, coef_y0 * coef_y1) rule.add_coef(y1, y0, coef_y1 * coef_y0) rule.add_coef(y1, y1, coef_y1 * coef_y1) # this is for (-4 + -5) y0 rule.add_coef(y0, y0, (-4 + -5) * coef_y0) # this is for (-4 + -5) y1 rule.add_coef(y1, y1, (-4 + -5) * coef_y1) rule.add_constant(4 * 5) for a in range(A): for w in range(D // 7): y1 = get_variable_id_y(D, A, T, a, w, 1) # this is for -y1 rule.add_coef(y1, y1, -1) return rule.finalize()Click to Copy
Since DA API is not opened to public, you must call "solveDA" function with BinaryQuadraticPolynomial object as the parameter. This "solveDA" will be swapped to make actual call to DA API when you submit your code.
def build_scheduling_rule(D, A, T, worker_skill, daily_workload, reqs, W):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
total_workload_rule = build_total_workload_rule(D, A, T, worker_skill, daily_workload)
preferred_time_rule = build_preferred_time_rule(D, A, T, reqs)
preferred_time_rule.multiply_constant(W)
workonce_rule = build_workonce_rule(D, A, T)
workonce_rule.multiply_constant(W)
sleep_rule = build_sleep_rule(D, A, T)
sleep_rule.multiply_constant(W)
holiday_rule = build_holiday_rule(D, A, T)
holiday_rule.multiply_constant(W)
rule.add_poly(total_workload_rule)
rule.add_poly(preferred_time_rule)
rule.add_poly(workonce_rule)
rule.add_poly(sleep_rule)
rule.add_poly(holiday_rule)
return rule.finalize()
def solveDA(rule):
'''This is a placeholder'''
print(rule.export_dict())
def main(D, A, T, worker_skill, daily_workload, reqs, W):
qubo = build_scheduling_rule(D, A, T, worker_skill, daily_workload, reqs, W)
return solveDA(qubo), qubo # wrapper to call DA API and return results and QUBO.
During the evaluation, we will call your "main" function with static parameters (D=7, A=25, T=4, W=95, and a static test case) to execute
your script.
To run your script locally, add following to verify your script;
if __name__ == "__main__":
D = 7
A = 25
T = 4
W = 95
seed = 1
worker_skill, daily_workload, reqs, W = generate_test_case(D, A, T, seed)
main(D, A, T, worker_skill, daily_workload, reqs, W)
Create a single python script file, zip it, and submit to Topcoder platform during the submission phase. The platform will run your script and return the results via email. Make sure that your email registered with Topcoder is accurate and up to date.
Due to how platform is hooked up with DA API, your scripts will be run one by one with other participants’ script. This means that your script will be put in a FIFO queue to run, and you might not be getting the results back immediately.
Following are several rules that apply to this challenge;
-
You can only run scripts that are intended to solve the provided learning
challenges and the Marathon Match.
The platform will be checking your scripts and returns error if the number of solution bits do not match what's mentioned in this tutorial or the returning energy is too low.
-
Each member can make maximum of 30 submissions for this challenge.
Please go ahead and try to submit multiple times. - The first 30 members to win a prize will be chosen after the submission phase is over.
Once you have submitted the script, the system will send you multiple emails that it has successfully received your script and performed virus checks. After your script has been executed against DA, the system will send you another email with results from "TC3-QuantumScorer" reviewer. When successful, the result of DA API will be provided in addition to the Schedule image that got solved. In case of error you will see a message of possible reasons, please try again to re-submit.
Note: When you get the solution back, you might notice that the products produced is a bit bigger/smaller amount than desired.
This is because we are using the same penalty weight (\( W \)) for all 5 formulae in this tutorial, and have tuned the DA API
parameters so that it gives the best solution when \( W=95 \). Thus, minimizing the number of workers would weigh larger than
the desired products produced.
You will be learning to tune the parameters to get better results in the next learning challenge #3 - Max-Cut, where you will
be able to more freely code and get desired solutions.
Please ask in the challenge forums if there are any questions.
Proposed Solution
As the submission phase for this tutorial #2 has ended, we are showing the proposed entire script provided for your reference.
'''
Step 1. Generate a scheduling task
'''
def generate_test_case(D, A, T, seed):
'''There are D days, A workers, T time slots per day, and the random seed is seed'''
assert D % 7 == 0, '[Error] D must be a multiple of 7 days'
np.random.seed(seed)
worker_skill = np.random.randint(5, 15, size = A)
# print 'worker_skill:', worker_skill
daily_workload = np.random.randint(15, 20, size=D)
daily_workload = 10 * daily_workload
# print 'daily_workload:', daily_workload
reqs = np.random.randint(2, size =(A, D, T))
W = np.max(daily_workload) // 2
# print 'W:', W
return worker_skill, daily_workload, reqs, W
'''
Step 2. Create a Helper Object that can be used to define QUBO
'''
import numpy as np
from math import sqrt
import copy
class BinaryQuadraticPolynomial:
'''Quadratic Polynomial class
Arguments:
n: The number of binary variables that can be handled by this quadratic polynomial. The variables are numbered from 0 to n - 1.
Attributes:
array: The numpy array showing this quadratic polynomial. array[i][j] (i <= j) is the coefficient of x_i * x_j. Since all variables are binary, x_i and x_i * x_i are the same variable.
constant: The constant value of this quadratic polynomial.
'''
def __init__(self, n = 1024):
self.array = np.zeros((n, n), dtype = int)
self.constant = 0
self._size = n
def export_dict(self):
'''Convert this quadratic polynomial to a dictionary. This is will be called in the DA Solver.'''
cells = np.where(self.array != 0)
ts = [{"coefficient": float(self.array[i][j]), "polynomials": [int(i), int(j)]} for i, j in zip(cells[0], cells[1])]
if self.constant != 0:
ts.append({"coefficient": float(self.constant), "polynomials": []})
return {'binary_polynomial': {'terms': ts}}
def add_coef(self, i, j, c):
if i > j: # make sure it is an upper triangle matrix.
t = i
i = j
j = t
assert i >= 0, '[Error] Index out of boundary!'
assert j < self._size, '[Error] Index out of boundary!'
self.array[i][j] += c
def add_constant(self, c):
self.constant += c
def add_poly(self, other_quad_poly):
assert self._size == other_quad_poly._size, '[Error] Array sizes are different!'
self.array += other_quad_poly.array
self.constant += other_quad_poly.constant
def multiply_constant(self, c):
self.array *= c
self.constant *= c
def finalize(self):
return copy.deepcopy(self)
'''
Step 3. Build Objective Function
'''
def get_variable_id(D, A, T, d, a, t):
'''x_{a,d,t}'''
return (d * A + a) * T + t
def get_variable_id_y(D, A, T, a, w, p):
'''y_{a,w,p=0/1}'''
return A * D * T + (w * A + a) * 2 + p
def get_total_varialbes(D, A, T):
return D * A * T + D // 7 * A * 2;
def build_total_workload_rule(D, A, T, worker_skill, daily_workload):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
for d in range(D):
# (sum(s_a x_{a,d,t}) - S_d)^2
S_d = daily_workload[d]
for t1 in range(T):
for a1 in range(A):
var1 = get_variable_id(D, A, T, d, a1, t1)
s_a1 = worker_skill[a1]
for t2 in range(T):
for a2 in range(A):
var2 = get_variable_id(D, A, T, d, a2, t2)
s_a2 = worker_skill[a2]
# s_a1 * s_a2 * x_{var1} * x_{var2}
rule.add_coef(var1, var2, s_a1 * s_a2)
# this is for -2 S_d s_a1 x_{var1}
rule.add_coef(var1, var1, - 2 * s_a1 * S_d)
rule.add_constant(S_d * S_d)
return rule.finalize()
def build_preferred_time_rule(D, A, T, reqs):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
for d in range(D):
for t in range(T):
for a in range(A):
var = get_variable_id(D, A, T, d, a, t)
# this is for (1 - reqs[a][d][t]) * x_{var}
rule.add_coef(var, var, 1 - reqs[a][d][t])
return rule.finalize()
def build_workonce_rule(D, A, T):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
for d in range(D):
for a in range(A):
# sum(x_{a, d, t}) * (sum(x_{a, d, t}) - 1)
for t1 in range(T):
var1 = get_variable_id(D, A, T, d, a, t1)
for t2 in range(T):
var2 = get_variable_id(D, A, T, d, a, t2)
rule.add_coef(var1, var2, 1)
# this is for -x_{var1}
rule.add_coef(var1, var1, -1)
return rule.finalize()
def build_sleep_rule(D, A, T):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
for d in range(D):
for a in range(A):
# x_{a, d, T - 1} * x_{a, d + 1, 0}
var1 = get_variable_id(D, A, T, d, a, T - 1)
# Note that this schedule will be repeated.
# So the next day of the last day is the first day.
var2 = get_variable_id(D, A, T, (d + 1) % D, a, 0)
rule.add_coef(var1, var2, 1)
return rule.finalize()
def build_holiday_rule(D, A, T):
# within each week, every worker works at most 5 days.
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
for a in range(A):
for w in range(D // 7):
y0 = get_variable_id_y(D, A, T, a, w, 0)
y1 = get_variable_id_y(D, A, T, a, w, 1)
coef_y0 = 2
coef_y1 = 5
# (sum(x_{a, d, t}) + 2y0 + 5y1 - 4) * (sum(x_{a, d, t} + 2y0 + 5y1 - 5))
for d1 in range(w * 7, w * 7 + 7):
for t1 in range(T):
var1 = get_variable_id(D, A, T, d1, a, t1)
for d2 in range(w * 7, w * 7 + 7):
for t2 in range(T):
var2 = get_variable_id(D, A, T, d2, a, t2)
rule.add_coef(var1, var2, 1)
rule.add_coef(var1, y0, 2 * coef_y0)
rule.add_coef(var1, y1, 2 * coef_y1)
# this is for (-4 + -5) x_{var1}
rule.add_coef(var1, var1, -9)
rule.add_coef(y0, y0, coef_y0 * coef_y0)
rule.add_coef(y0, y1, coef_y0 * coef_y1)
rule.add_coef(y1, y0, coef_y1 * coef_y0)
rule.add_coef(y1, y1, coef_y1 * coef_y1)
# this is for (-4 + -5) y0
rule.add_coef(y0, y0, (-4 + -5) * coef_y0)
# this is for (-4 + -5) y1
rule.add_coef(y1, y1, (-4 + -5) * coef_y1)
rule.add_constant(4 * 5)
for a in range(A):
for w in range(D // 7):
y1 = get_variable_id_y(D, A, T, a, w, 1)
# this is for -y1
rule.add_coef(y1, y1, -1)
return rule.finalize()
def build_scheduling_rule(D, A, T, worker_skill, daily_workload, reqs, W):
rule = BinaryQuadraticPolynomial(get_total_varialbes(D, A, T))
total_workload_rule = build_total_workload_rule(D, A, T, worker_skill, daily_workload)
preferred_time_rule = build_preferred_time_rule(D, A, T, reqs)
preferred_time_rule.multiply_constant(W)
workonce_rule = build_workonce_rule(D, A, T)
workonce_rule.multiply_constant(W)
sleep_rule = build_sleep_rule(D, A, T)
sleep_rule.multiply_constant(W)
holiday_rule = build_holiday_rule(D, A, T)
holiday_rule.multiply_constant(W)
rule.add_poly(total_workload_rule)
rule.add_poly(preferred_time_rule)
rule.add_poly(workonce_rule)
rule.add_poly(sleep_rule)
rule.add_poly(holiday_rule)
return rule.finalize()
def solveDA(qubo):
'''This is a placeholder'''
print(qubo.export_dict())
def main(D, A, T, worker_skill, daily_workload, reqs, W):
qubo = build_scheduling_rule(D, A, T, worker_skill, daily_workload, reqs, W)
return solveDA(qubo), qubo # wrapper to call DA API and return results and QUBO.
if __name__ == "__main__":
D = 7
A = 34
T = 4
seed = 1
worker_skill, daily_workload, reqs, W = generate_test_case(D, A, T, seed)
main(D, A, T, worker_skill, daily_workload, reqs, W)